受限制玻尔兹曼机(Restricted Bolzmann Machine)以及自编码器(Autoencoder)

受限制玻尔兹曼机(Restricted Bolzmann Machine, RBM)与自编码器(Autoencoder, AE)是神经网络的两种基本结构，两个结构都能起到降维的作用，都可以用来对神经网络进行预训练（pre-training），这种预训练都是无监督的。由于RBM与MLP及其相似，一直以来我就困惑于他们两者，终于花了几天时间来搞清楚他们的区别和训练方法，发现他们甚至不是并列的关系。。

一、知识脉络

受限制玻尔兹曼机 -> 深度信念网络(Deep Blief Network, DBN)

自编码器 -> 堆叠自编码器(Stacked Autoencoderm, SAE)

二、自编码器

自编码器的输入维度与输出维度相等，训练目的是使数据的特征得到最大的保留，去除冗余信息，一个单层的自编码器结构如下图

AE3

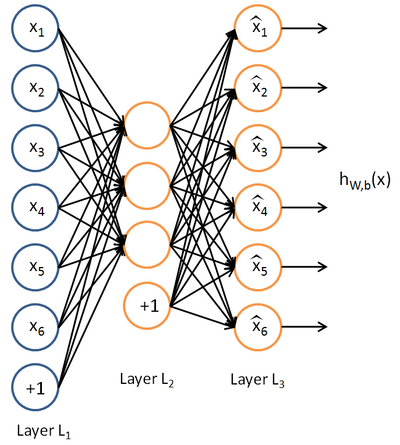
当然一个自编码器也可以有很多层：

AE1

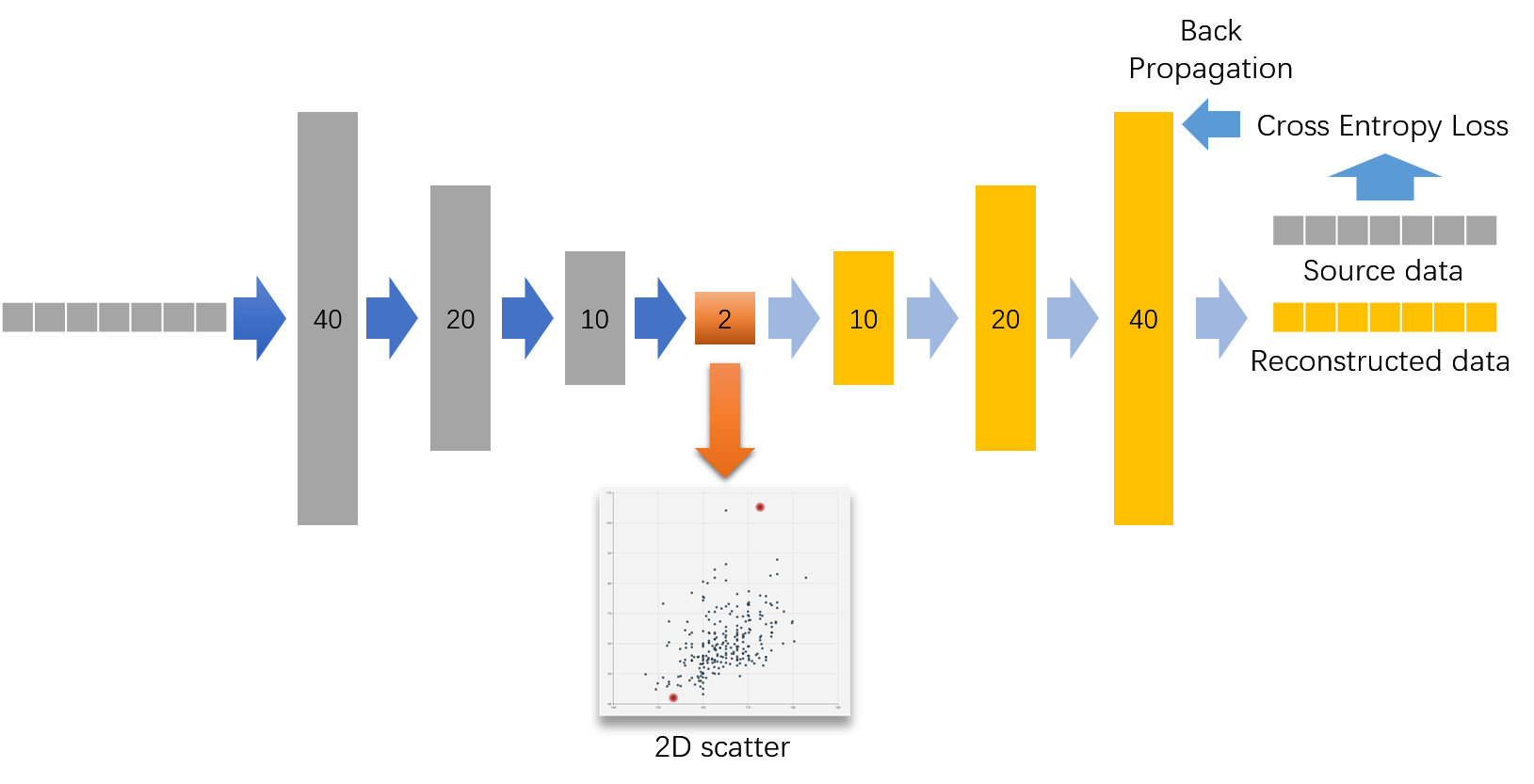
简化来看就是输入层->隐藏层->输出层，自编码器的目的就是使重建(reconstruction)的输出层能尽量还原输入层，同时获得中间隐藏层(最窄的橙色那层)既是降维的结果。若输入层到隐藏层间的部分称为编码器(灰色)，记号为f(x)，隐藏层到输出层之间的部分称为解码器(黄色)，记号为g(x)，那么自编码器的数学训练目标就是

eq1

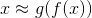
三、受限制玻尔兹曼机

受限制玻尔兹曼机是一个双层结构，可见层(visible)与隐藏层(hidden)，图结构为一个二分图，即可见层只与隐藏层之间有连接，但是层内是无连接的，因此RBM的性质：当给定可见层神经元的状态时，各隐藏层神经元的激活条件独立；反之当给定隐藏层神经元的状态时，可见层神经元的激活也条件独立。基本结构如下

RBM1

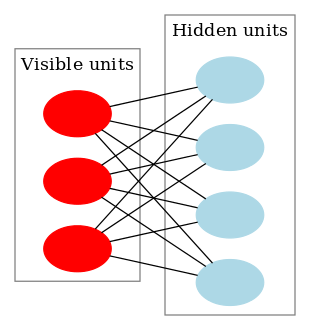
受限制玻尔兹曼机的训练目的是为了最大程度的保留概率分布，定义了一个能量函数的概念

$E（v，h）= - \ sum_i a_i v_i - \ sum_j b_j h_j - \ sum_i \ sum_j v_i w_ {i，j} h_j$

用矩阵来表示就是

$E（v，h）= -a ^ {\ mathrm {T}} v -b ^ {\ mathrm {T}} h -v ^ {\ mathrm {T}} W h$

a与b分别是可视层与隐藏层的偏置项(bias)

v, h联合概率分布是

$P（v，h）= \ frac {1} {Z} e ^ { - E（v，h）}$

其中Z是所有[v, h]对对应的能量的总和，v的边缘概率分布如下，h同理

$P（v）= \ frac {1} {Z} \ sum_h e ^ { - E（v，h）}$

由于受限玻尔兹曼机结构上的特点，所以各隐藏层之间的神经元条件概率独立，即

$P（h | v）= \ prod_ {j = 1} ^ n P（h_j | v）$

可见层v同理

$P（v | h）= \ prod_ {i = 1} ^ m P（v_i | h）$

能量函数的具体推导过程将会在后面的文章中详细解释

四、训练方法

就像RBM是由物理模型转化过来一样，训练方法与传统的反向传播(BP)也不一样

RBM最早的训练方法有Gibbs sampling，通过不断地来回采样来训练，如下图

gibbs

然而这样的方法太慢，所以Hinton大神又提出了CD-k(contrastive divergence)算法，即只需要来回重复k次就可以，以CD-1为例:

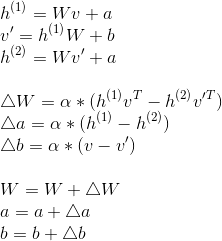
就可以完成一次迭代，这就像是两种不同温度的液体进行混合，如果两者的温度差距较大，在混合的过程中就会产生较大的梯度，而受限制玻尔兹曼机的训练目标就是使得两边的“温度”能够尽量的相近，而在数据中这个“温度”的体现就是数据分布。也就是说，使用RBM进行模型的初始化训练能够最大程度的保留数据分布，防止梯度爆炸和梯度消失问题的出现。

五、深度信念网络与逐层训练

由多层受限制玻尔兹曼机堆叠起来的网络叫作深度信念网络(DBN)。深度信念网络在最后一层接入一个Softmax层用作分类，训练的时候采取逐层训练+微调的方式

逐层训练就是从输入层开始将网络的相邻两层当作一个受限制玻尔兹曼机进行无监督训练，训练方法见上一节，训练后将上一个RBM的隐藏层当作下一个RBM的可见层继续
逐层无监督训练完毕后，将进行反向传播训练对模型进行微调，从输入端输入数据，最后从输出端开始进行反向传播

AE2

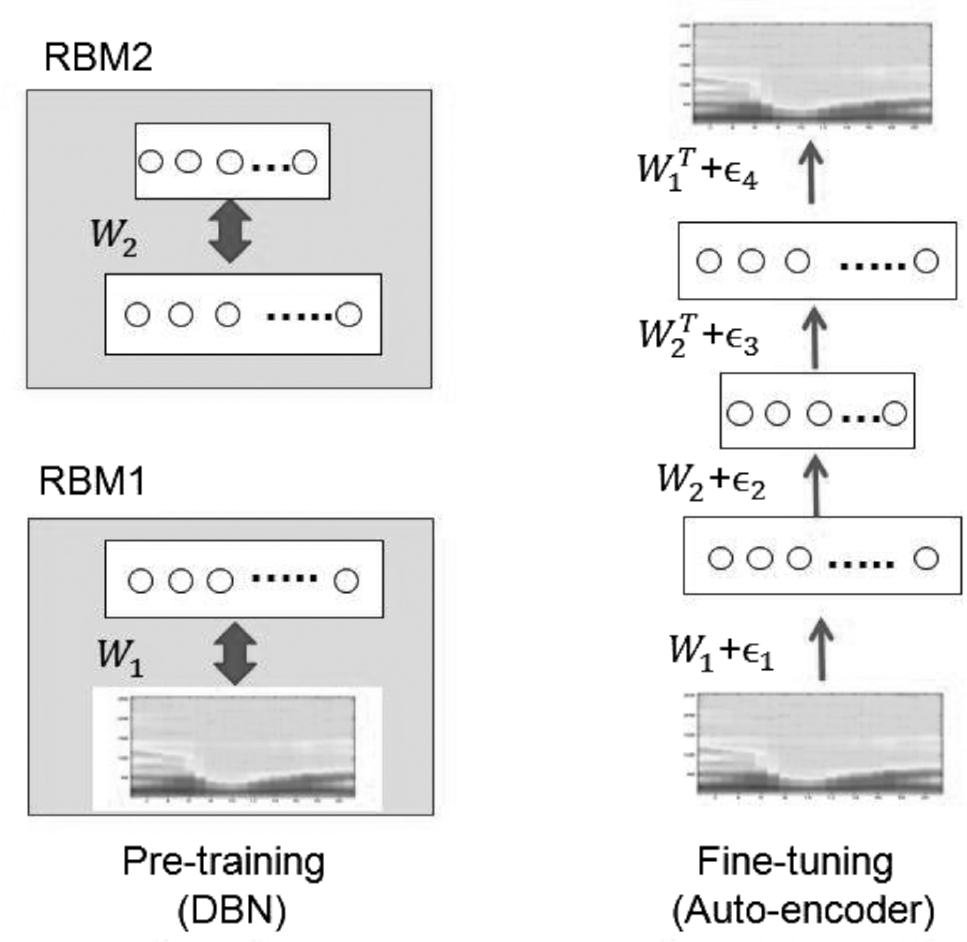
自编码器虽然只是要保证输出端与输入端尽量接近，但是随着自编码器堆叠深度的加深，就会出现类似梯度弥散与梯度爆炸等问题，Hinton大神同样也使用了类似RBM的训练方法对深度自编码器进行逐层训练，使模型的得到了很好的初始化，加快了模型的解的最优性和收敛速度。

六、参考

受限玻尔兹曼机与深度置信网络

Hinton G E. A practical guide to training restricted Boltzmann machines[M]//Neural networks: Tricks of the trade. Springer, Berlin, Heidelberg, 2012: 599-619.
Bengio Y, Lamblin P, Popovici D, et al. Greedy layer-wise training of deep networks[C]//Advances in neural information processing systems. 2007: 153-160.
Hinton G E, Osindero S, Teh Y W. A fast learning algorithm for deep belief nets[J]. Neural computation, 2006, 18(7): 1527-1554.
Hinton G E, Salakhutdinov R R. Reducing the dimensionality of data with neural networks[J]. science, 2006, 313(5786): 504-507.