在前面的一篇文章 受限制玻尔兹曼机(Restricted Bolzmann Machine)以及自编码器(Autoencoder)中我们提到了RBM的能量函数这一概念以及对比散度(CD)的快速采样的训练方法,但我一直纠结与为何Hinton大神能够从能量函数和Gibbs Sampling中获得CD-k采样算法,两个式子看似没有关联。于是我花了几天的时间,终于对RBM这个结构有了更深一步的了解。
一、能量函数与概率分布
之前讲到受限制玻尔兹曼机时,我们提到,RBM是由一个可见层(visible, v)与隐藏层(hiddenm, h)组成,如下图,W在物理中表示系统内部能量转换,比如分子间碰撞产生的能量传递,同时有a, b两个偏置项,在物理中表示外来因素的影响,与外界的能量交换:
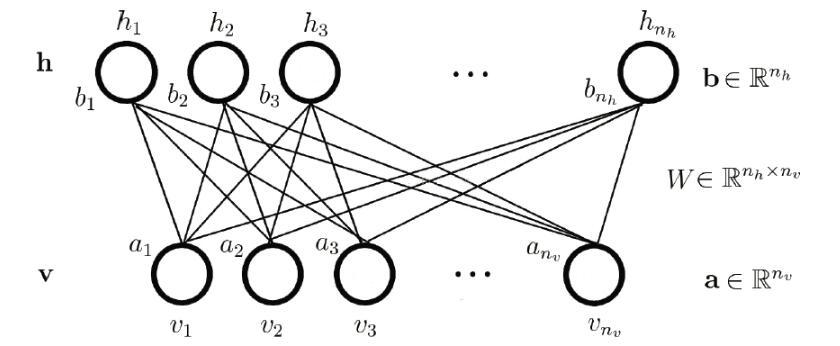
能量函数的定义是:
用矩阵来表示就是
能量函数具体的含义涉及物理领域,在本文不会具体介绍,具体请阅读Ising Model的相关文章,本文具体介绍如何从能量函数中推倒出Gibbs Sampling和CD-k
v, h联合概率分布是
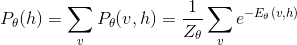
其中Z是所有[v, h]对对应的能量的总和,称为归一化因子或配分函数(Partition Function)
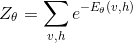
v与h的边缘概率分布如下
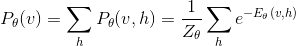
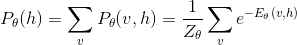
条件分布
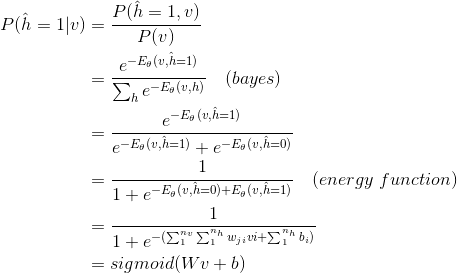
同理
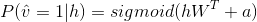
由于RBM层内无连接,所以同一层内的变量还具有相互独立性,即
二、对数似然函数
上面定义了那么多,然而要开始正式的梯度优化,我们还差一个优化目标,现在就要正式地定义损失函数:
之前曾经提到过,受限制玻尔兹曼机的训练目的是让原始数据的分布得到最大的保留,用最大似然估计来表示就是让P(v)最大。采用对数似然函数,则式子如下:
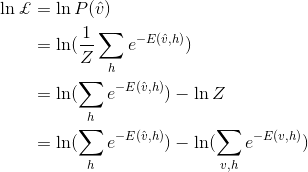
对参数求梯度:
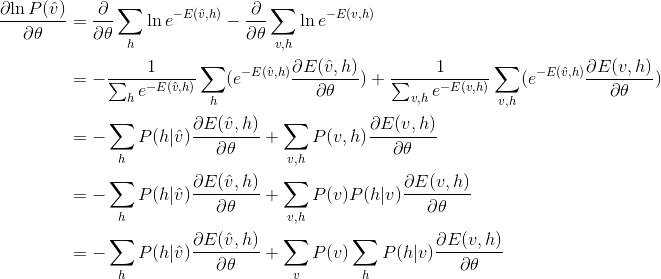
所以只要能求得 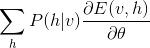
就可以求出最终的梯度,RBM每层有W, a, b三个不同的参数,则需要分别对三个参数分别求导:
W
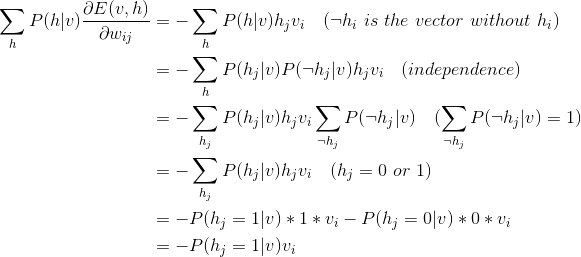
b与W的推导过程类似,结果为:
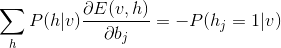
a的推导更加的简单
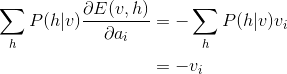
把上面三个式子带回到梯度的公式中,就可以得到
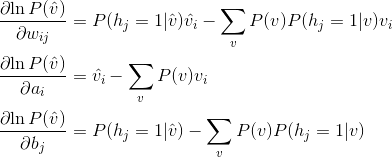
这就是Gibbs采样和CD-k采样的来源,只是采用了不同的估计方法来确定概率分布。



