Xavier方法用于神经网络参数初始化

Posted on | In | 阅读

之前我们学习了使用RBM对深度置信网络进行逐层训练初始化，或用类似的方法对多层深度神经网络进行预训练(pretraining)，以求最终收敛的结果接近最优且加快收敛速度，同时还能避免梯度消失(gradient vanishing)和梯度爆炸(gradient explosion)的问题。今天介绍一个更加方便快速的初始化方法，来近似达到相同的目的。

一、梯度消失与梯度爆炸

这是一个深度学习领域遇到的老问题了，即使是现在，任何一个新提出的模型，无论是MLP、CNN、还是RNN，随着深度的加深，这两个问题变得尤为严重。

  • 梯度消失是指在深度学习训练的过程中，梯度随着链式求导逐层传递逐层减小，最后趋近于0，导致对某些层的训练失效；
  • 梯度爆炸与梯度消失相反，梯度随着链式求导逐层传递逐层增大，最后趋于无穷，导致某些层无法收敛；

出现梯度消失和梯度爆炸的问题主要是因为参数初始化不当以及激活函数选择不当造成的，这在之后我会做相应的笔记来讨论batch normalization与激活函数

二、Xavier方法

接下来的推导基于假设:

  • 激活函数在0周围的导数接近1(比如tanh);
  • 偏置项b初始化为0，期望为0
  • 参数初始化期望均为0

显然，在初始化参数的时候不能全部初始化为0，这样无论是什么输入，输出都是0，无法训练，但也不能随意去初始值，否则就会造成梯度不稳定的问题。那么什么样的初始值才是合适的呢？

答案就是使每层的分布都尽量相等，RBM就是为了这个目的而训练的，但是Xavier做了进一步的简化：保留均值(可以在下一层开始的时候再做调整)与方差

对于每一个输出的神经元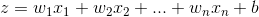Z

都要使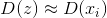approx

又

Dz

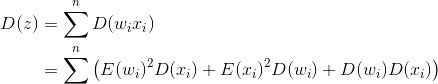
根据假设E(w)与E(x)均等0且所有w与x同分布，则：

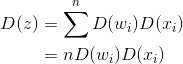
Dzshort

要满足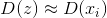approx所以:

Dw

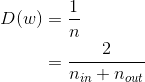
其中nin与nout分别是输入层与输出层的神经元个数

如果W服从正态分布，那么这就是所需要的参数，但如果假设W服从均匀分布，那么

result

但是之前有假设激活函数在0周围的导数接近1，所以忽略了激活函数的作用，不同激活函数在0周围的导数不同，需要给方差乘上导数的倒数

Activation Function Uniform Distribution
sigmoid 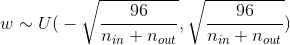96
tanh 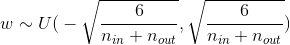6
ReLU 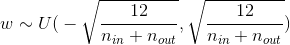12

三、代码实现

tensorflow的实现

1
2
3
4
def xavier_init(fan_in, fan_out, constant = 1):
    low = -constant * np.sqrt(6.0 / (fan_in + fan_out))
    high = constant * np.sqrt(6.0 / (fan_in + fan_out))
    return tf.random_uniform((fan_in, fan_out), minval=low, maxval=high, dtype=tf.float32)

完整代码里实现了一个使用Xavier方法初始化的单层自编码器