线性判别分析(LDA)

线性判别分析(Linear Discriminant Analysis, LDA)是另外一种线性降维方法。与主成分分析法不同，线性判别分析是一种有监督学习，也就意味着线性判别分析需要使用带标签的数据进行训练来完成降维。

主成分分析法笔记

---

的主要思想是找到一种线性映射至低维空间的方法，保证降维后带有不同标签的数据能够尽量分散，而带有相同标签的数据能够尽量相互集中，与PCA一样，分散这一评价指标仍然由方差来决定。

1. 二分类情况

   考虑当样本的类别只有两类(0和1)且从d维映射至一维的问题，如下图

   

   LDA的优化目标

   

   其中μ_i为第i类样本的中心点，∑_i表示第i类样本的协方差矩阵，即(x-μ_i)(x-μ_i)^T; w即需要找到的最佳映射方式

   定义“类内散度矩阵”(within-class scatter matrix)

   

   以及“类间散度矩阵”(between-class scatter matrix)

   

   则优化目标可以写为

   

   称为S_b和S_w的“广义瑞利商”(generalized Rayleigh quotient)

   但是只有这个式子是不够的，因为当w乘以一个倍数的时候，答案J不会改变，就有无穷多解。要求唯一解，就要对w进行限制，限制之后的优化目标：

   

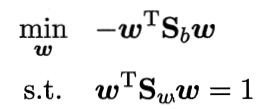
   与PCA相同，通过拉格朗日乘子法，得到：

   

   

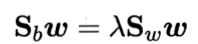
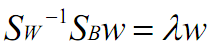
   又

   

   

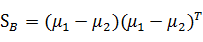
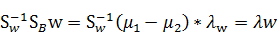
   由于w的任何倍数不会影响结果，所以

   

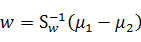
   我们只要求出S_w就可以出最优的w

   ​

2. 多分类情况

   多分类情况下，需要定义“全局散度矩阵”：

   

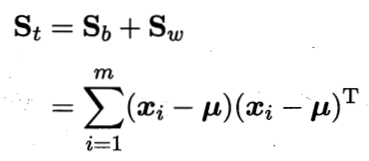
   类内散度与类间散度矩阵的规定不变

   

   

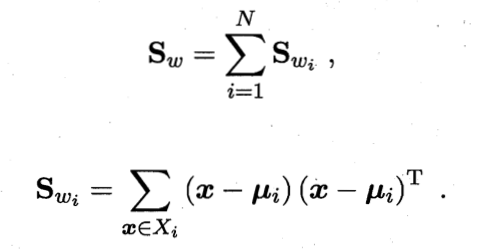
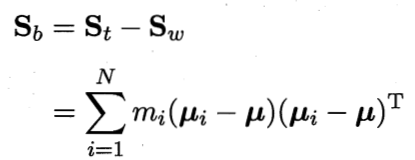
   只要知道其中的两者利用广义瑞利商就可以算出最优解，例如按照二分类的方法得到

   

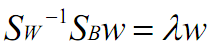
   同样也能求出解;