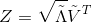多维缩放(MDS)

多维缩放(multidimensional scaling ,MDS)，是另外一种线性降维方式，与主成分分析法和线性降维分析法都不同的是，多维缩放的目标不是保留数据的最大可分性，而是更加关注与高维数据内部的特征。多维缩放算法集中于保留高维空间中的“相似度”信息，而在一般的问题解决的过程中，这个“相似度”通常用欧式距离来定义。

假设D为m个样本在高维空间中的距离矩阵，dist_ij为第i个样本与第j个样本的欧式距离

Z是样本在低维中映射的表示，那么，多维缩放的降维目标就是要保证：

令B=Z^TZ，B为降维后样本的内积矩阵，b_ij=z_i^Tz_j

规定降维后的样本为中心化样本，因为只保留了距离信息，无论结果怎么旋转、平移都可以，即

那么

令

综合以上各式，得到

所以可以使用距离矩阵D来求得内积矩阵B，

为了完成降维，可以将B进行特征值分解

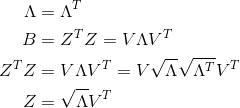
仅保留最大的前d’个特征值以及相应的特征向量，就可以得出降维后的结果