t-SNE(基于t分布的随机近邻嵌入,t-distributed stochastic neighbor embedding),是Laurens van der Maaten大神在Geffory Hinton大神的SNE基础上加入t分布而形成的,是目前效果最好的可视化降维算法,可以将高维数据内部的特征放大,使得相似的数据在低维中能更加接近,不相似的数据在低维中距离更远。
一、SNE
SNE由Hinton大神在2003年提出,它提出的目的就是为了改进MDS与ISOPMAP寻求距离完全按照原有维度内的问题,转而满足高低维之间满足分布上的统一。虽然这样会导致距离信息有了一定程度的丢失,但是这么做保留了距离的分布,获得更好的可视化效果。
SNE需要通过训练使得高维与低维的距离的高斯分布尽量的接近,即:
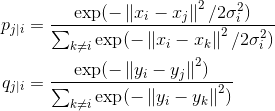
满足高维的点在p中的值与低维的q中的值能够尽量接近,cost函数采用KL散度:
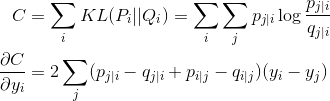
采用动量优化的方式进行训练
二、Symmetric SNE
传统的SNE的分布映射方法不具有对称性,即pi|j与pj|i不相等,所以可以将映射方式改成联合概率分布的方式:
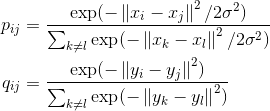
但是高维中的离群点的cost就会很低,因为它离所有点的距离都非常的远,p非常小,所以,可以把p改写成
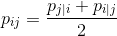
这样cost的值就改写为:
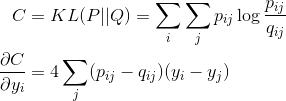
三、t-SNE
之前所说的各种算法中,都会产生拥挤问题,所谓拥挤问题就是高维数据中的距离关系不能完整地在低维空间中得以保留,10维中可以有11个点相互等距,而二维空间中最多就只能有3个点组成等边三角形,这样的降维肯定不能够保证距离的保留。同时可以参考这篇博客中的实验,同样是均匀分布会发现高维空间中均匀分布的点中距离分布也是很不均匀的,随着维度的增大,距离越远的点的比重会越来越大。
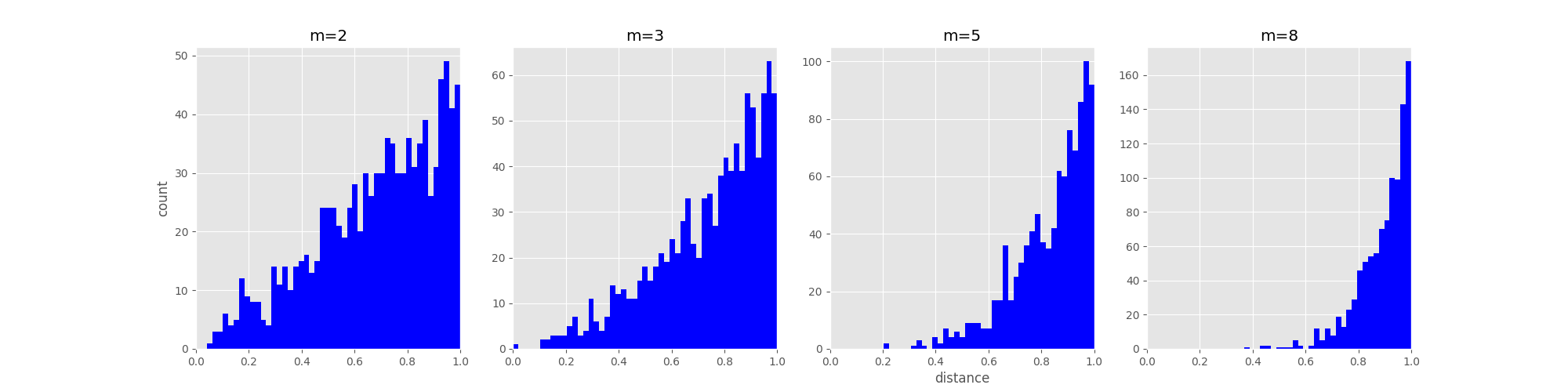
所以,如果不设法减轻这种拥挤问题,那么就会出现高维空间中距离较远与较近的点,在低维中的距离相同的问题,使得类与类之间分不开。为解决拥挤问,T分布就能够一展神通。
T分布具有长尾的特性,即碰到有离群点时,不会因为离群点使整个分布脱离原有的大部分数据,同时,低维数据使用T分布映射而高维数据使用正态分布作为映射,如下图:
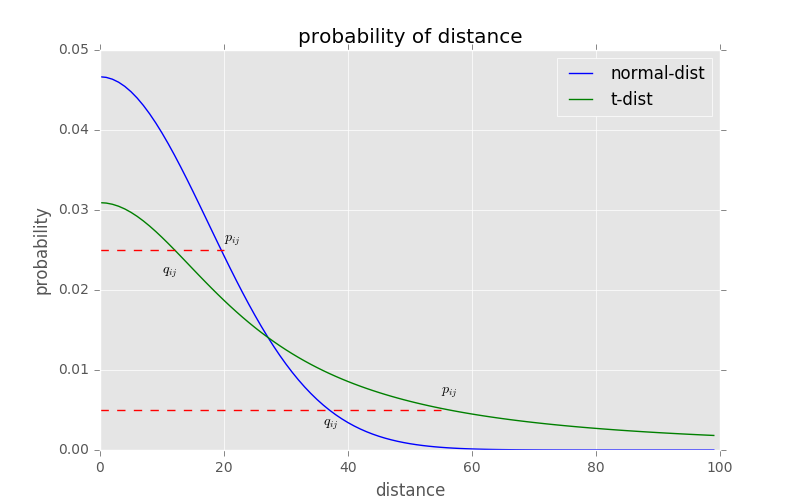
在高维空间中较近的点在低维空间中将会更近,而较远的点将会更远,这样就能有效缓解拥挤问题,tsne的公式为
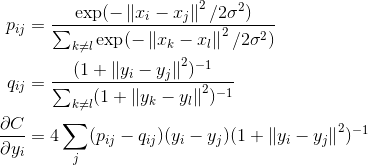
tsne结果:
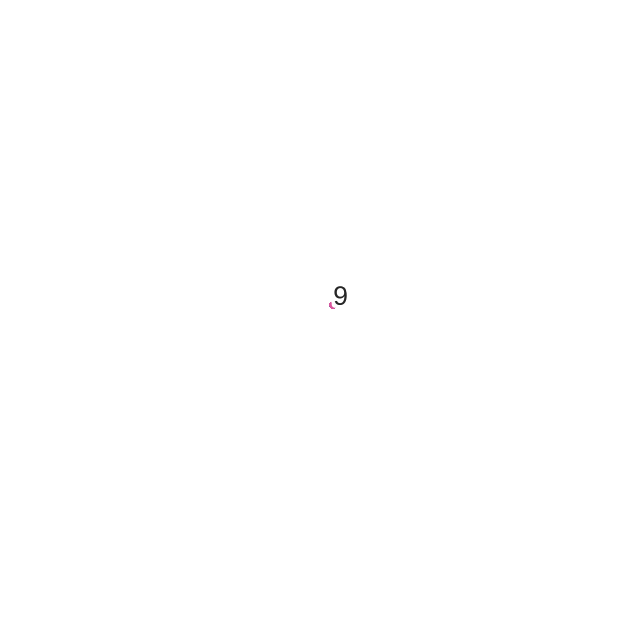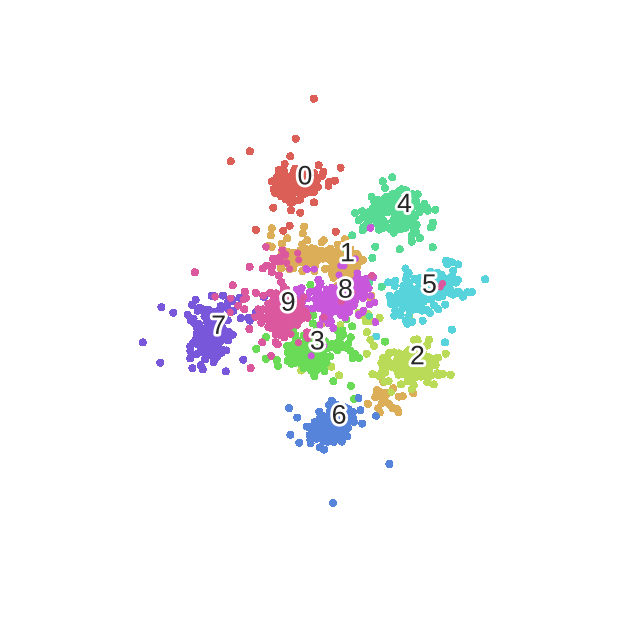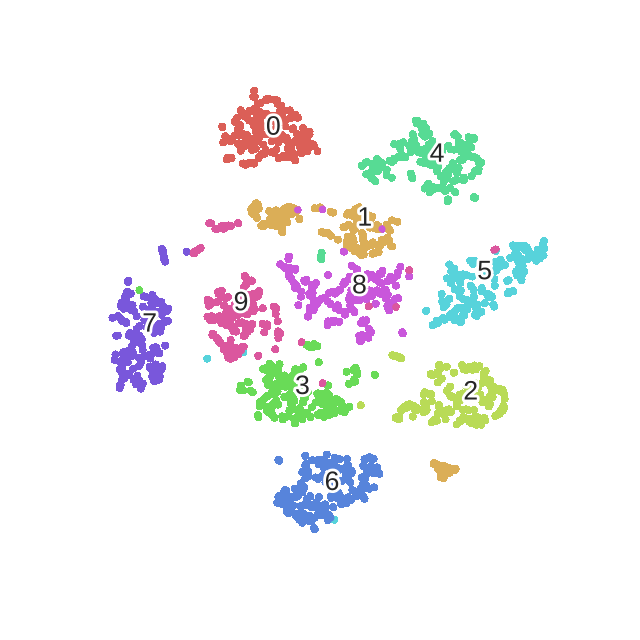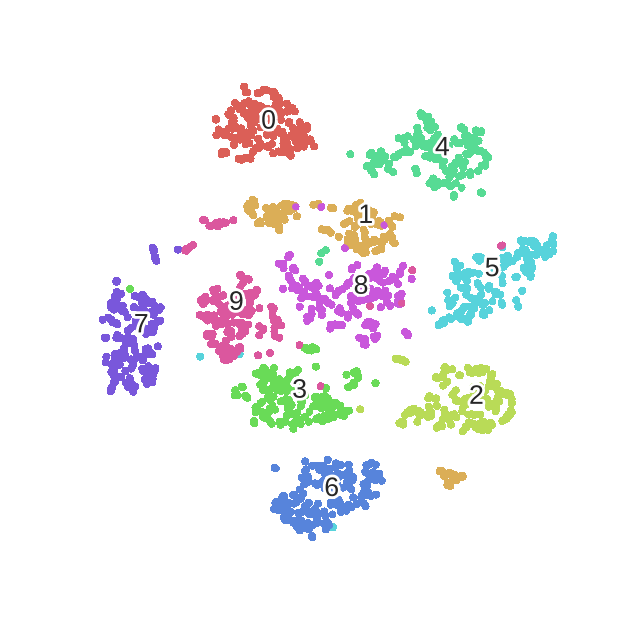
参考
- Maaten L, Hinton G. Visualizing data using t-SNE[J]. Journal of machine learning research, 2008, 9(Nov): 2579-2605.
- Hinton G E, Roweis S T. Stochastic neighbor embedding[C]//Advances in neural information processing systems. 2003: 857-864.