马氏距离(Mahalanobis Distance)是度量学习中一种常用的距离指标,同欧氏距离、曼哈顿距离、汉明距离等一样被用作评定数据之间的相似度指标。但却可以应对高维线性分布的数据中各维度间非独立同分布的问题。
什么是马氏距离
马氏距离(Mahalanobis Distance)是一种距离的度量,可以看作是欧氏距离的一种修正,修正了欧式距离中各个维度尺度不一致且相关的问题。
单个数据点的马氏距离
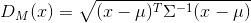
数据点x, y之间的马氏距离
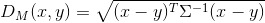
其中Σ是多维随机变量的协方差矩阵,μ为样本均值,如果协方差矩阵是单位向量,也就是各维度独立同分布,马氏距离就变成了欧氏距离。
马氏距离实际意义
那么马氏距离就能能干什么?它比欧氏距离好在哪里?举几个栗子
欧式距离近就一定相似?
先举个比较常用的例子,身高和体重,这两个变量拥有不同的单位标准,也就是有不同的scale。比如身高用毫米计算,而体重用千克计算,显然差10mm的身高与差10kg的体重是完全不同的。但在普通的欧氏距离中,这将会算作相同的差距。
归一化后欧氏距离近就一定相似?
当然我们可以先做归一化来消除这种维度间scale不同的问题,但是样本分布也会影响分类
举个一维的栗子,现在有两个类别,统一单位,第一个类别均值为0,方差为0.1,第二个类别均值为5,方差为5。那么一个值为2的点属于第一类的概率大还是第二类的概率大?距离上说应该是第一类,但是直觉上显然是第二类,因为第一类不太可能到达2这个位置。
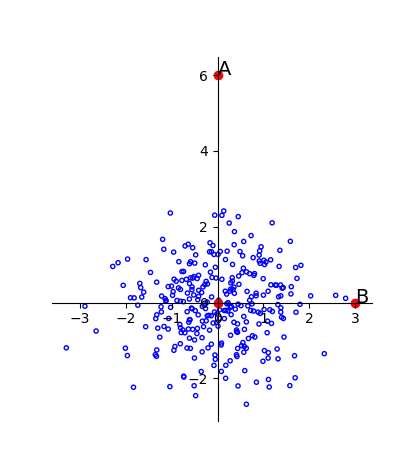
所以,在一个方差较小的维度下很小的差别就有可能成为离群点。就像下图一样,A与B相对于原点的距离是相同的。但是由于样本总体沿着横轴分布,所以B点更有可能是这个样本中的点,而A则更有可能是离群点。
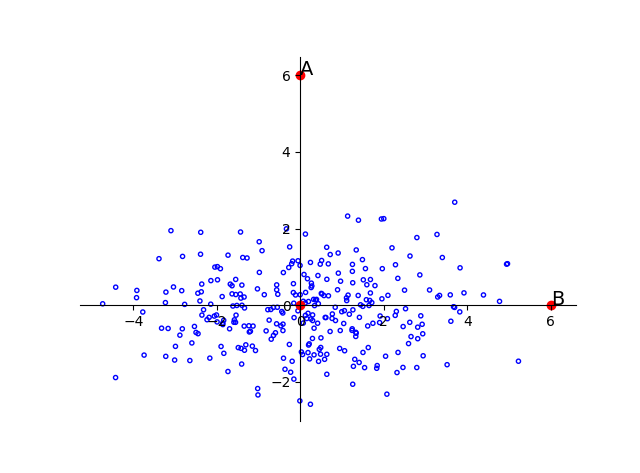
算上维度的方差就够了?
还有一个问题——如果维度间不独立同分布,样本点一定与欧氏距离近的样本点同类的概率更大吗?
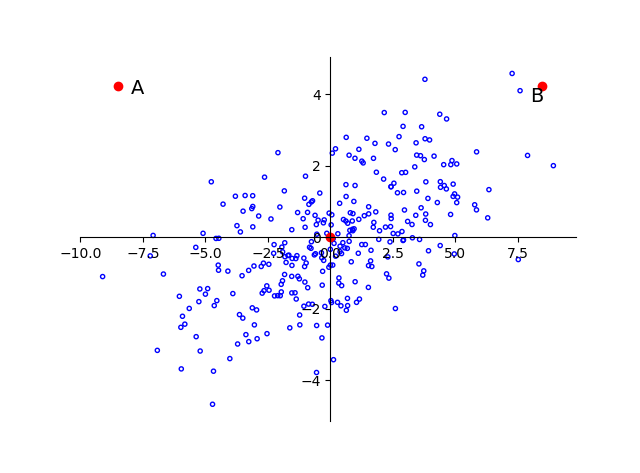
可以看到样本基本服从f(x) = x的线性分布,A与B相对于原点的距离依旧相等,显然A更像是一个离群点
即使数据已经经过了标准化,也不会改变AB与原点间距离大小的相互关系。所以要本质上解决这个问题,就要针对主成分分析中的主成分来进行标准化。
马氏距离的几何意义
上面搞懂了,马氏距离就好理解了,只需要将变量按照主成分进行旋转,让维度间相互独立,然后进行标准化,让维度同分布就OK了
由主成分分析可知,由于主成分就是特征向量方向,每个方向的方差就是对应的特征值,所以只需要按照特征向量旋转,然后缩放特征向量倍就可以了,可以得到以下的结果:
离群点就被成功分离,这时候的欧式距离就是马氏距离。
马氏距离的推导
首先要对数据点进行旋转,旋转至主成分,维度间线性无关,假设新的坐标为
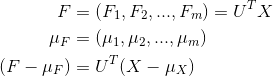
又变换后维度间线性无关且每个维度自己的方差为特征值,所以满足:
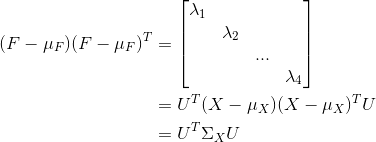
马氏距离是旋转变换缩放之后的欧式距离,所以马氏距离的计算公式为:
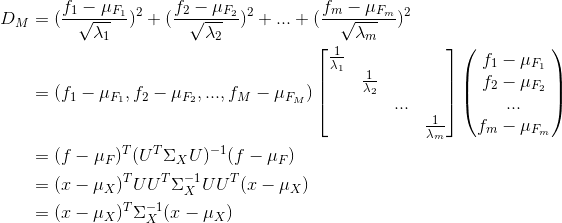
这就是之前提到的马氏距离的公式
马氏距离的问题
协方差矩阵必须满秩
里面有求逆矩阵的过程,不满秩不行,要求数据要有原维度个特征值,如果没有可以考虑先进行PCA,这种情况下PCA不会损失信息
不能处理非线性流形(manifold)上的问题
只对线性空间有效,如果要处理流形,只能在局部定义,可以用来建立KNN图